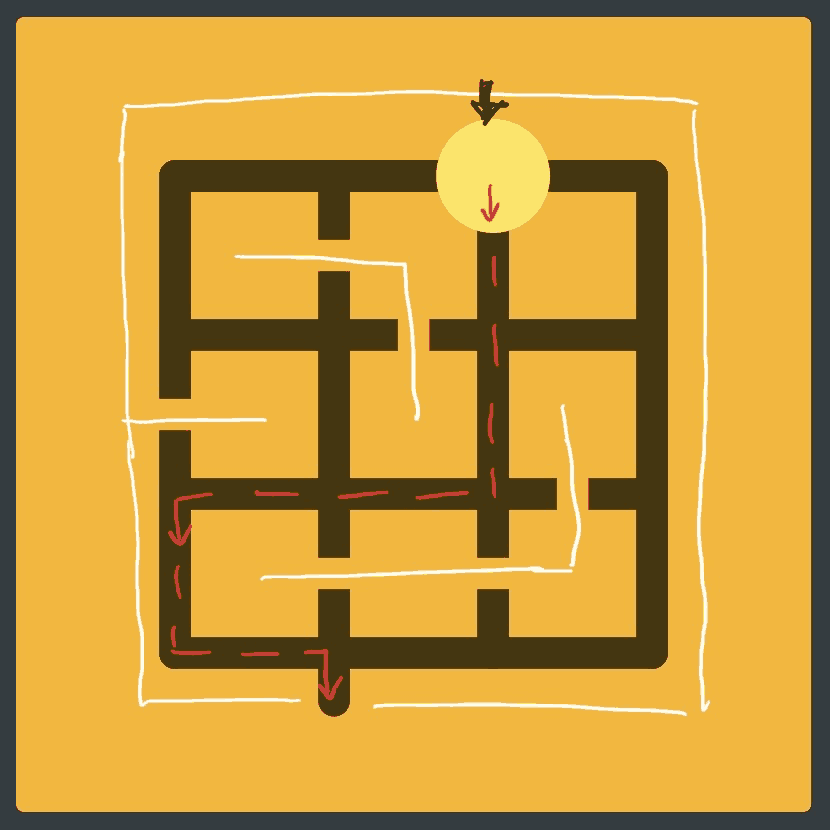
Building a useful CLI tool is a proven way to try a new programming language. That is unless the language is designed specifically for the browser. In the latter case, developing a simple video game can make for a fun alternative. Back in 2015, I built a minimalistic Tetris clone while learning ClojureScript, and more recently I’ve been looking for a challenge to try the latest version of Elm (0.19). The inspiration struck when I thought about The Witness: a 2016 video game by Jonathan Blow, which shifted my opinion about the puzzle games and stuck in my memory as one of the most powerful pieces of digital art I’ve ever witnessed (bad pun intended). There’s a concealed area in the late game, where you’re given a limited time to solve a bunch of puzzle panels which, unlike all previously encountered ones, are generated procedurally. One type of puzzle you might face is a maze that looks like this:

Without committing to any overly ambitious goals (although, I admit, the thought of implementing all different kinds of in-game panels has crossed my mind), I agreed to build at least this simple panel. During the initial research, I discovered that most of the readily available sources on maze generation focus on perfect mazes (no loops and a single solution) and assume an imperative programming language with mutable data structures and easy access to randomness. Elm, on the other hand, is a pure functional programming language that disallows any side-effects (e.g., generating a random number is typically a side effect). For a moment, I entertained the thought that the project I picked might not be best suited to the language’s strengths, but I shushed the doubts away and proceeded. In the end, I did face some difficulties along the way, and I didn’t arrive at my final approach right from the start, but the search was a rewarding experience in itself. Now, you can try and play the resulting game (which is, admittedly, not very entertaining), or continue and read about how it works (which is, of course, very much fun). I promise some cool (by the standards of this blog) Elm-powered SVG animations.

The Witness’ mazes are inverted, meaning that they’re defined in terms of paths and not walls. Thus, you can think of paths as gaps and “broken” paths as walls. I made a quick drawing to illustrate this point.

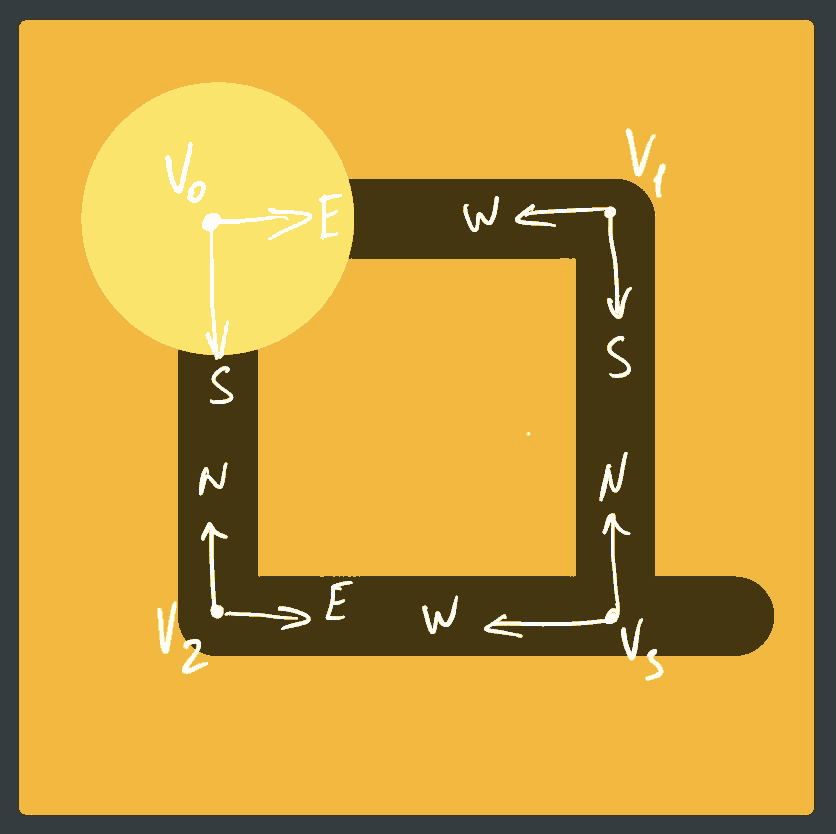
The textbook data structure for representing a rectangular maze is a two-dimensional array of encoded connections for each square. I didn’t want to deal with array indexes, hoping to get more benefit from the type system this way, so I instead went with a custom abstract graph data type, which I call a quadgraph. A quadgraph is a unidirectional cyclic graph where each node might be connected to up to four other nodes. I labeled these four (indexed) edge “slots” as north, east, south, and west. The “slots” must be connected symmetrically, such as edge a has a north edge to b if and only if b has a south edge to a; and edge b has an east edge to d if and only if d has a west edge to b. Again, look at the illustration below to get a sense of what I mean:

In Elm, such graph can be represented by utilizing the built-in dictionary type Dict as an adjacency list, where the keys are numeric node identifiers, and the values are just special record types:

type alias QuadGraph a e =
    Dict NodeId (Node a e)


type alias NodeId =
    Int


type Edge e
    = Edge NodeId NodeId e


type alias Node a e =
    { id : NodeId
    , value : a
    , north : Maybe (Edge e)
    , east : Maybe (Edge e)
    , south : Maybe (Edge e)
    , west : Maybe (Edge e)
    }

To stay true to Computer Science, we’re allowing for two type parameters: a for values held in graph vertices, and e for values in edges. For the maze panel, we won’t need a at all, but e can be utilized to store the path state: either broken or intact. For better readability, one might decide to use a custom type such as Path = Intact | Broken, but I chose to go with a boolean type where true stands for a passable edge and false for a “broken” one:

type alias MazeGraph =
    QuadGraph () Bool

While we could implement an algorithm to determine the width (west to east) and height (north to south) of any given quadgraph, it’s more efficient to store them alongside the graph in a record type:

type alias Grid =
    { graph : MazeGraph
    , width : Int
    , height : Int
    }

Even though we’re not using a two-dimensional array, we can still benefit from encoding the positional coordinates of nodes within the grid into their identifiers as follows:

nodeId = row * grid.width + col

Finally, we can put all these pieces together and generate a graph for the initial rectangular grid.

newGrid : Int -> Int -> Grid
newGrid width height =
    let
        cols =
            List.range 0 (width - 1)

        rows =
            List.range 0 (height - 1)

        disconnectedGraph =
            List.range 0 (width * height - 1)
                |> List.foldl (\id graph -> QuadGraph.insertNode id () graph) QuadGraph.empty
    in
    { graph =
        rows
            |> List.concatMap (\i -> List.concatMap (buildConnections i) cols)
            |> List.foldl (<|) disconnectedGraph
    , width = width
    , height = height
    }

If we render the panel now, it’ll be in the state shown below. Please note a subtle distinction between having an edge between two nodes and such an edge being “intact”. For example, the top left node is missing the west and the south edges, while all its other edges are “broken”.

Before we can carve some paths in our maze, we need to pick a random starting node. Randomness is one of the aspects that make Elm different from other languages, including some functional languages. In Elm, you normally describe the kind of random value you want using a special type called generator, and then ask the Elm runtime to call your code back with the generated value. This, arguably more complex, process comes with the benefit of keeping your own code free of random side effects and also translates into some very expressive code for certain uses. For our current task at hand, we just need a generator that returns a random node identifier from a list:

randomStartPoint : MazeGraph -> Random.Generator NodeId
randomStartPoint graph =
    graph
        |> QuadGraph.nodeIds
        |> randomListElement -1


randomListElement : a -> List a -> Random.Generator a
randomListElement default list =
    case list of
        x :: xs ->
            Random.uniform x xs

        _ ->
            Random.constant default

An extra attentive reader might see that I “cheated” here: the Elm’s randomness API is smart enough to require a non-empty list when asking to produce a uniformly distributed value from a list. But since dealing with empty graphs is outside of the scope of this exercise, I use a shortcut of returning -1 as a nodeId to avoid dealing with Maybe here.

Now it’s time to carve the paths, and this is also where things get a little more complicated. Most graph algorithms rely on some mutable state to track whether a particular node was already visited or not. In a pure language like Elm, our best bet is passing such state around, which can make the code more than a little convoluted, since the state has to be passed as an argument to every function call and returned with every return value. Combined with recursion, it’s a sure way to introduce some weird errors into your program and make debugging difficult. Luckily, there is a community library called elm-state that makes this process a little less tedious via some clever tricks that originated in Haskell. I won’t go into too much detail on that, but essentially it allows one to thread a piece of state through a computation, hiding away the complexities of carrying it backwards and forwards throughout a tree of recursive function calls. Using elm-state, it’s relatively straightforward to define common operations such as map and fold that work on cyclic graphs and hide these complexities from the API user. One important note, though: one cannot just fold a graph unless she picks the start node and defines which edges are traversable. Let’s define one additional type to express that:

type Foldable a e
    = Foldable (e -> Bool) NodeId (QuadGraph a e)

This new Foldable type accepts a function that takes an edge value and returns a boolean (traversable or not), a starting node identifier, and the underlying graph. Our custom versions of fold will work on this type instead of the “bare” QuadGraph a e. I wasn’t entirely honest though, because what we’re after is not a regular fold, but a function that traverses the graph depth-first, picking nodes at random,… while modifying the graph at every step (sheesh!). The type definition for it might look like this:

module QuadGraph.Traverse.Random exposing (runDepthFirst)

runDepthFirst : (List NodeId -> NodeId -> QuadGraph a e -> QuadGraph a e) -> Foldable a e -> Random.Generator (QuadGraph a e)

Internally, it uses elm-state to thread the following state through its traversal of the graph:

type alias RunState a e =
    { graph : QuadGraph a e
    , visited : Set NodeId
    , currentSeed : Random.Seed
    }

On every step, the algorithm moves one node further, continuing until it can no longer move (think, Snake), at which point it backtracks and covers other paths. The illustration below shows how this works step by step. Look at how the “splits” form and how there is never more than a single path out of the start node.

What we have now is called a perfect maze: if we take any end of the maze, there will be one and only one path to it from the inception point, and no loops. Essentially, we’ve just carved a tree within our graph. That said, The Witness maze panels have loops, and thus, so must we. Also, what would be the point of using a full-blown graph data structure for representing a mere tree? Luckily, the algorithm of carving loops is “dead-end simple” (speaking of bad puns): find all dead-ends and add an extra edge connecting those nodes to one of their neighbors.

One way of finding dead ends can be expressed using a depth-first fold of our graph where we record every node with just a single connection:

findDeadEnds : MazeGraph -> NodeId -> List NodeId
findDeadEnds graph startNodeId =
    QuadGraph.Traverse.foldDepthFirst
        (\path nodeId deadEnds ->
            let
                connectionsCount =
                    nodeId
                        |> QuadGraph.get graph
                        |> Maybe.map connectedNodes
                        |> Maybe.withDefault []
                        |> List.length
            in
            if connectionsCount <= 1 then
                nodeId :: deadEnds
 
            else
                deadEnds
        )
        []
        (QuadGraph.Foldable identity startNodeId graph)

We can then carve a loop from every dead by marking a random broken edge as intact:

carveLoops : MazeGraph -> NodeId -> Random.Generator MazeGraph
carveLoops inputGraph startNodeId =
    let
        deadEnds =
            findDeadEnds inputGraph startNodeId

        carveLoop deadEnd graph =
            let
                targetsGenerator =
                    deadEnd
                        |> QuadGraph.get graph
                        |> Maybe.map disconnectedNodes
                        |> Maybe.withDefault []
                        |> Random.List.shuffle
            in
            targetsGenerator
                |> Random.map List.head
                |> Random.map (Maybe.map (\nodeId -> QuadGraph.updateEdge deadEnd nodeId True graph) >> Maybe.withDefault graph)
    in
    List.foldl (carveLoop >> Random.andThen) (Random.constant inputGraph) deadEnds

Some of the edges might end up being modified twice, but that only means a maze with fewer loops, which is a welcome variation. The process of carving loops is illustrated below:

Now that we have a maze, we can walk it from the start point in every direction (i.e., breadth-first), looking for a path that is the longest (or just long enough to be challenging). And, finally, this is our chance to use fold on the graph:

buildRoute : MazeGraph -> Int -> NodeId -> List NodeId
buildRoute graph minAcceptableLength startNodeId =
    let
        vertexDistances =
            QuadGraph.Traverse.foldBreadthFirst
                (\path nodeId distances -> Dict.insert nodeId (nodeId :: path) distances)
                Dict.empty
                (QuadGraph.Foldable identity startNodeId graph)
    in
    vertexDistances
        |> Dict.toList
        |> List.sortBy (Tuple.second >> List.length >> min minAcceptableLength)
        |> List.reverse
        |> List.map Tuple.second
        |> List.filter (\solution -> solution |> List.head |> Maybe.andThen (QuadGraph.get graph >> Maybe.map QuadGraph.isLeaf) |> Maybe.withDefault False)
        |> List.head
        |> Maybe.withDefault []

Note how the exit is always on the outside edge of the maze, which also limits the search scope. I’ve found that paths three times the maze longer dimension or longer are usually the most fun on smaller mazes. However, with my current algorithm, there’s no guarantee that such a path is going to be present in the maze.

And this is how the maze is made. You can play the resulting game (keyboard is required), browse the source, or, if you feel adventurous, try changing some code and see if the compiler complaints. The latter is a great way to become more familiar with Elm.

P.S. For those who read until here, here’s a bonus tip: press + to increase the maze size in both demo and playable modes of the game. Now you can make a “you’ll never escape this maze” bet with a friend or watch the “AI” do it… Because these are the things people actually do.

I’d like to acknowledge the work of Jamis Buck, whose articles on maze generation algorithms have been invaluable to me while working on this little project. I originally started with my own approach, but changed almost everything after reading “Maze Generation: Recursive Backtracking” and some other articles on his blog. This is good content!